Введение в теорию управления
Во многих производственных процессах выходную переменную объекта управления (например, температуру, давление или расход) требуется поддерживать постоянной или изменять по заданному закону. В подобных случаях обычно система управления строится
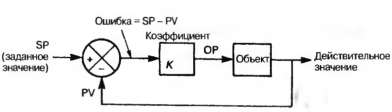
по принципу, иллюстрируемому на рис. 4.27, где действительное значение переменной объекта с помощью обратной связи сравнивается с ее желаемым (заданным) значением. Такая система называется системой с обратной связью, или замкнутой системой.
При сравнении заданного значения переменной, обозначаемого SP (от английского Setpoint — уставка), с ее действительным значением PV (от английского Process Variable) образуется ошибка Е, т. е.
Умножение ошибки на коэффициент К дает выходной сигнал управляющего устройства ОР:
Воздействие этого сигнала на объект является причиной изменения PV. В случае безынерционного объекта сигнал PV будет прямо пропорционален ОР, т. е. мы можем записать
где А — обычный коэффициент усиления.
Выражения (4.7)—(4.9) позволяют сразу получить зависимость
т. е. выходной сигнал объекта PV просто будет равен уставке SP, умноженной на масштабирующий коэффициент АК/{\ + АК). Член АК называют коэффициентом усиления разомкнутой системы и часто обозначают через G, поэтому можно записать
Можно видеть, что при больших значениях G разность между PV и SP будет достаточно малой. Например, при G = 10 мы получим PV = 0.91SP. Большие значения G можно обеспечить увеличением коэффициента усиления К. К сожалению, на практике это часто приводит к неустойчивости системы. Проблему устойчивости мы обсудим в следующем разделе.
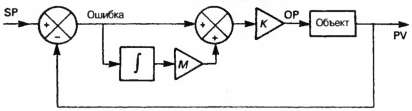
На рис. 4.28 представлен модифицированный тип стратегии управления, когда сигнал ОР образуется как сумма ошибки и интеграла по времени от ошибки, т. е.
По очевидным соображениям такой закон управления называют пропорционально-интегральным, или ПИ-законом.
Интегральный член будет заставлять ОР изменяться до тех пор, пока существует ошибка, а когда ошибка станет равной нулю (при SP = PV), ОР примет постоянное значение. Таким образом, ПИ-регулятор в установившемся режиме будет обеспечивать нулевую ошибку без необходимости увеличения коэффициента усиления.
В регуляторах, применяемых на практике, коэффициент М в выражении (4.12) заменяется на 1/Тi):
где Тi,- — время (постоянная) интегрирования. Необходимость такой замены обусловлена чисто математическими соображениями.
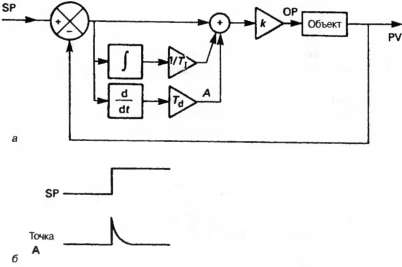
Дальнейшая модификация структуры системы управления приведена на рис. 4.29. Здесь дополнительно введена компонента производной по времени, пропорциональная скорости изменения ошибки, в результате чего мы имеем
Нет ничего удивительного в том, что такой трехканальный регулятор называют ПИД-регулятором (т. е. пропорционально-интегрально-дифференциальным). Множитель Td известен как время (постоянная) дифференцирования.
Наличие канала дифференцирования выгодно по двум причинам. Поскольку он реагирует на скорость изменения ошибки, то при резком скачке уставки он будет давать на выходе «бросок» сигнала, как показано на рис. 4.29 (б). За счет дифференцирования также улучшается устойчивость системы и уменьшается перерегулирование.
Пока что мы рассмотрели случай, когда выходной сигнал объекта должен был отслеживать уставку. Но замкнутый контур управления полезно иметь тогда, когда объект подвержен внешним возмущениям, как показано на рис. 4.30. Например, в системе управления уровнем таким возмущением может быть изменение выходного потока, в системе управления температурой — Изменения температуры окружающей среды и нагреваемого материала, в системе управления расходом — изменение напора. Поскольку все
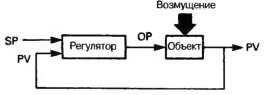
подобные возмущения приводят к изменению сигнала PV, регулятор будет реагировать на это и стремиться так скорректировать управляющий сигнал ОР, чтобы восстановить равенство PV = SP и тем самым устранить влияние возмущения.