Периодичность преобразования

Преобразование сигнала из аналоговой в цифровую форму не происходит мгновенно (хотя в цифровом телевидении используются сверхбыстродействующие АЦП, обладающие временем преобразования в единицы наносекунд). В большинстве промышленных систем есть большая вероятность помех, наложенных на сигнал от линий переменного тока (с частотой 50 или 60 Гц в зависимости от страны).

Часто периодичность преобразования привязывается к частоте сети переменного тока, что дает высокую степень подавления помех от этой сети. При этом периодичность преобразования составляет 20 мс в Великобритании (частота сети 50 Гц) и 16.67 мс в США (частота сети 60 Гц).

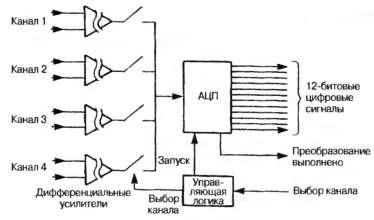
В случае четырехканального мультиплексора каждый канал опрашивается по очереди, поэтому выборки сигнала будут производиться с периодом 80 мс. Если аналоговая плата находится в удаленной стойке, то к этому времени надо добавить время прогона программы и время доступа к плате.

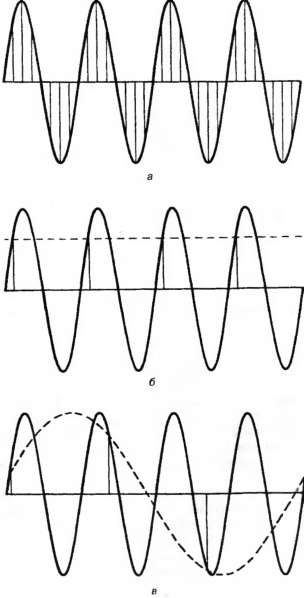
Аналоговая входная плата производит мгновенные выборки сигналов, поступающих от объекта. Кроме значений этих выборок, никакой другой информации о сигналах не существует. Как показано на рис. 4.17 (а) и 4.17 (б), если выборки производятся с одним и тем же периодом, то оба сигнала (разные!) дадут одинаковый результат, приведенный на рис. 4.17 (<?). Поэтому возникает естественный вопрос: как следует выбирать частоту квантования непрерывного сигнала, чтобы его дискретные значения точно представляли форму исходного сигнала?

На рис. 4.18 (а) синусоидальный сигнал квантуется с достаточно высокой частотой. Интуитивно можно предположить, что эта частота является приемлемой. На рис. 4.18 (б) частота квантования совпадает с частотой сигнала. Ясно, что в этом случае частота квантования является слишком низкой, так как получаемые выборки соответствуют постоянному сигналу.

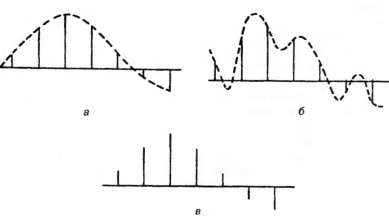
На рис. 4.18 (в) частота квантования меньше частоты сигнала, и по значениям выборок можно составить представление, что речь идет о синусоиде с частотой, много меньшей, чем у исходного сигнала. Этот эффект называется смещением частоты. Его можно визуально наблюдать на экране кинотеатра, когда колеса автомобиля часто кажутся вращающимися в обратную сторону. Это происходит из-за того, что кинокамера делает снимки окружающей обстановки примерно 50 раз в секунду.

Любой непрерывный сигнал занимает определенную полосу частот. Чтобы по выборкам можно было достаточно точно восстановить форму исходного сигнала, частота квантования должна быть по крайней мере в два раза больше полосы частот, занимаемой непрерывным сигналом. Такова, в несколько упрощенном виде, формулировка импульсной теоремы Шеннона.

Ни одна реальная система, конечно, не может иметь конкретной полосы пропускания и резко обозначенной частоты среза. Шумы и другие подобные эффекты приводят к тому, что на полезный сигнал будут накладываться составляющие более высоких частот. Из-за этих составляющих может возникать упомянутое выше смещение частоты. Поэтому перед квантованием любой сигнал необходимо пропустить через низкочастотный фильтр, чтобы гарантировать, что квантованию подвергается только сигнал, занимающий определенную полосу частот.

Большинство сигналов в системах управления занимают полосу частот в несколько герц, поэтому их квантование в соответствии с теоремой Шеннона не вызывает особых проблем. Обычно эта полоса заранее не известна, поэтому используется частота квантования, которая в 5—10 раз больше предполагаемой полосы частот, занимаемой сигналом. Например, для сигнала с частотой 2 Гц будет вполне достаточно квантовать его с частотой 10 Гц, что соответствует периоду 100 мс.

К счастью, подобные проблемы возникают редко. На практике промышленные системы, реальные сигналы в которых связаны с объектом, имеющим значительную массу, редко обладают полосой пропускания более 0.5 Гц; поэтому сигнал любой частоты, превышающей это значение, можно рассматривать как внешний шум, который должен быть отфильтрован. Например, в системах, содержащих тепловые объекты, сигналы часто можно квантовать с периодичностью всего один раз в несколько минут без внесения каких-либо ошибок. Проектировщик, однако, всегда должен быть уверен, что выполняется импульсная теорема Шеннона и что время преобразования АЦП совместимо с измеряемыми сигналами.