Комбинаторная логика

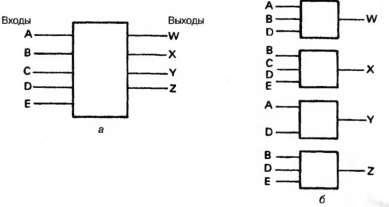
Любую систему управления, работающую с цифровыми сигналами, можно представить в виде рис. 2.44 (а), где состояния выходных сигналов Z, Y, X, W и т. д. определяются значениями входов А, В, С, D и т. д. Работу системы управления можно организовать, используя комбинацию двух основных методов.

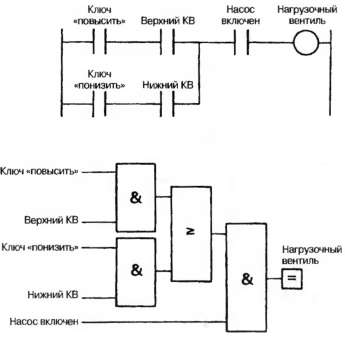
Самым простым из этих методов является комбинаторная логика, когда систему можно разбить на более мелкие блоки, как на рис. 2.44 (б), с одним выходом у каждого блока, причем состояние выхода определяется только значениями соответствующих входов. Например, нагрузочный вентиль гидравлического насоса будет задействован, если:

Работу этого нагрузочного вентиля можно организовать с помощью простой программы в виде многоступенчатой схемы или логической структуры, как на рис. 2.45, но предпочтительнее разработать стандартный способ создания программы на основе комбинаторной логики.

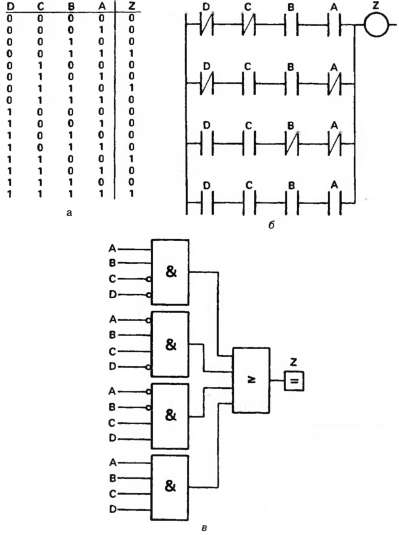
Первый этап заключается в разбиении системы управления на ряд небольших блоков, каждый из которых имеет один выход и несколько входов. Далее для каждого выхода надо составить так называемую таблицу истинности, в которой должны быть записаны все возможные состояния входов и соответствующие им требуемые состояния выхода. На рис. 2.46 (а) мы имеем выход Z, зависящий от четырех входов А, В, С, D. Всего имеется 16 возможных комбинаций состояний входов, a Z активизируется (т. е. является истинным) только для четырех из них. Это сразу можно отобразить в виде многоступенчатой схемы на рис. 2.46 (б) или логической схемы на рис. 2.46 (в), где каждое звено или вентиль AND соответствуют одной строке таблицы истинности.

Использование таблиц истинности для синтеза схем комбинаторной логики непосредственно приводит к структуре, состоящей из элементов AND/OR и на техническом языке называемой «суммой произведений».

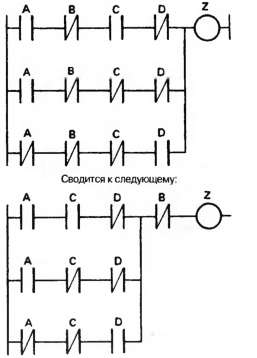
Возникает естественный вопрос: «Является ли такая структура простейшей?» Ответ будет отрицательным, так как существуют такие методы, как карты Карно и булева алгебра, дающие более простое решение. Если структура создается из логических вентилей или реле, то желательно обойтись минимальным количеством вентилей или контактов, чтобы снизить расходы на проектирование. При написании программы для ПЛК дополнительных контактов не требуется, поэтому главной целью должна быть прозрачность работы программы, а не ее простота. Одно из упрощений, которое всегда рекомендуется делать (опять же для прозрачности), заключается в вынесении из звеньев общего контакта, как показано на рис. 2.47.

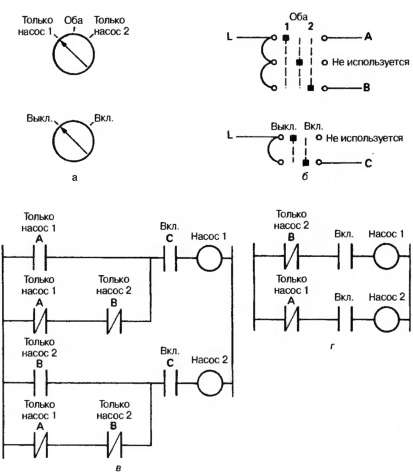
В качестве примера рассмотрим пульт управления приводом насосов, изображенный на рис. 2.48 (а). Ради дешевизны трехпозици-онный переключатель соединен напрямую с двумя группами контактов, как показано на рис. 2.48 (б) (на практике так делать не

рекомендуется, так как при отказе источника питания оба насоса будут включенными). Таблица истинности для этого случая приводит к многоступенчатой схеме на рис. 2.48 (в), но схема минимальной сложности имеет вид рис. 2.48 (г). Последняя, однако, не отражает работу переключателя и поэтому несколько затрудняет обнаружение неисправностей.