Представление чисел
До сих пор мы рассматривали только однобитовые операции. Однако в системах управления часто приходится иметь дело с числами. От ПЛК можно потребовать вычислить, сколько единиц продукции в среднем производится в час в течение рабочего дня, или определить количество жидкости в накопительной емкости. Для выполнения таких операций ПЛК должен обладать способностью обрабатывать числовые данные.
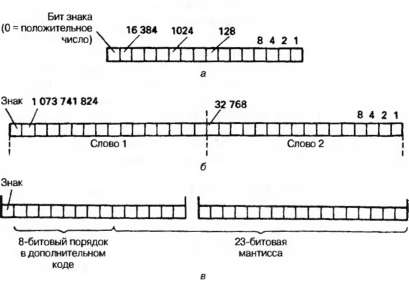
Большинство ПЛК работают с 16-битовым словом, позволяющим представлять положительные числа в диапазоне от 0 до +65 535 или числа со знаком (положительные или отрицательные) в диапазоне от —32 768 до +32 767 в дополнительном коде (см. Приложение). В последнем случае самый старший бит представляет знак числа, принимая значение 1 для отрицательных чисел и 0 — для положительных. В программах для ПЛК обычно (но не обязательно) используется представление чисел в дополнительном коде.
Числа, подобные приведенным выше, называются целыми и поэтому могут представлять только любое целое число в соответствующем диапазоне. Для получения большего диапазона представления целых чисел можно использовать два 16-битовых слова, при этом диапазон чисел составит от —2 147 483 648 до +2 147 483 647. Этот тип целых чисел доступен в ПЛК ABB Master (где их называют «длинными целыми») и в 135U и 155U семейства Siemens (где используется термин «целое слово двойной длины»).
Для представления десятичных дробей (например, чтобы получить значение температуры 45.6 °С) используются числа, которые всем известны по работе с обычным калькулятором. Они называются числами с плавающей точкой и обычно состоят из двух 16-битовых слов, содержащих мантиссу (цифровую часть) и порядок числа. Например, при основании 10 число 74 057 будет иметь мантиссу 7.4057 и порядок (показатель степени) 4, представляющий 10". Разумеется, ПЛК работают в двоичной системе, поэтому мантисса и порядок представляются в виде дополнительного двоичного кода. Среди производителей имеются неизбежные различия в представлении вещественных чисел, но самым новым стандартом является 32-битовый формат с одинарной точностью, установленный IEEE (американским Институтом инженеров по электротехнике и электронике). Этому стандарту соответствует рис. 2.35 (в), что позволяет получать диапазон чисел ±(от 1.175Е-38 до 3.402Е38). Некоторые производители жертвуют диапазоном порядка, чтобы получить большую точность для мантиссы. Например, в ABB Master диапазон чисел составляет +(от 5.4Е-20 до 9.2Е18), что дает более высокую точность.
Вещественные числа определенно полезны, однако следует четко представлять связанные с ними ограничения. Здесь имеются две проблемы. Первая возникает при совместном использовании больших и малых чисел. Предположим, что мы имеем систему, работающую с основанием 10 с четырьмя значащими цифрами, и хотим сложить 857 800 (записанное как 8.578Е5) и 96 (записанное как 9.600Е1). Поскольку меньшее число находится вне диапазона (четыре значащие цифры) большего, оно будет проигнорировано, в результате чего получится 857 800 + 96 = 857 800.
Вторая проблема возникает, когда проверяется равенство вещественных чисел. Преобразование десятичных чисел в двоичные может быть выполнено с разрешением, обеспечиваемым форматом с плавающей точкой (1.175Е-38 в стандарте IEEE с одинарной точностью). Большинство домашних компьютеров хранят числа в формате с плавающей точкой, и может произойти то, что демонстрирует простая программа на языке BASIC:
110В=6.4
120 С=9.4
130 IF (А+В)=С THEN PRINT ("3+6.4=9.4"): GOTO 150
140 PRINT ("3+6.4 does not = 9.4, it =");: PRINT С
150 PRINT ("Take care with real numbers!")
Эта простая программа не делает того, что вы могли ожидать! При сравнении вещественных чисел использование знака равенства (=) очень важно. Безопаснее использовать составные знаки >= (больше или равно) и <= (меньше или равно), но предпочтительнее все же для проверки использовать целые числа, если это вообще возможно.
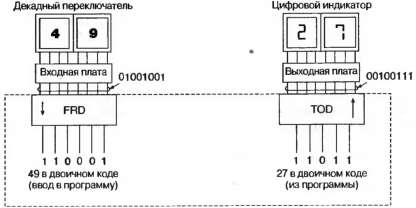
Последнее представление чисел — двоично-десятичное (BCD — binary coded decimal) — используется для связи с внешними устройствами, такими как цифровые индикаторы или барабанные переключатели с цифрами по образующей цилиндра. Такие устройства приспособлены для работы в десятичном формате, причем на декаду отводится 4 двоичных разряда. Данное представление является избыточным, так как 6 чисел (от 10 до 15 включительно) не используются при кодировании четырьмя битами. Однако это очень удобно для соединений с внешними устройствами. Поэтому большинство ПЛК снабжены инструкциями, которые преобразуют BCD во внутренний двоичный формат, а также двоичное представление обратно в BCD. Например, в PLC-5 имеются инструкции FRD (from decimal — преобразование десятичных чисел в двоичный формат) и TOD (to decimal — переход от двоичного представления к десятичному). На рис. 2.36 схематически приведен пример подобных операций. В разделах Преобразование двоично-десятичного числа в двоичное и Преобразование двоичного числа в двоично-десятичное описывается, как можно выполнить те же преобразования без использования указанных функций.
Используемые в каждом семействе ПЛК типы чисел значительно отличаются в зависимости от модели (и, разумеется, от цены). Например, в Mitsubishi F2 можно производить только перемещение, сравнение и вывод данных в цифровой форме от счетчиков или таймеров, что делает этот ПЛК по сути машиной с побитовыми операциями.
В семействе Siemens распространенная модель 115-U использует только 16-битовые целые числа, однако следующая модель семейства, 135-U, может обрабатывать 16-битовые и 32-битовые целые числа, а также числа с плавающей точкой. Аналогичное расширение возможностей можно обнаружить и в семействах Allen Bradley, GEM-80 и ABB.