Динамические характеристики датчика
В стационарных условиях датчик полностью описывается своей передаточной функцией, диапазоном измеряемых значений,калибровочными коэффициентами и т.д. Однакона практике выходной сигнал датчика не всегда достаточно точно отслеживает изменение внешнего сигнала. Причины: инерционностьсамого датчика и особенности егосоединения с источником внешних воздействий, не позволяющая сигналам распространяться с бесконечно большойскоростью.
Динамические характеристики- параметры датчика, зависящие от времени.
Динамические погрешности – погрешность датчика из-за ограниченности его быстродействия.Отличие между статическими и динамическими погрешностями - последние всегда зависят от времени.Если датчик входит в составизмерительного комплекса, обладающего определенными динамическими характеристиками, внесениедополнительных динамических погрешностей может привести, в лучшем случае, к задержке отображенияреального значения внешнего воздействия, а, в худшем случае, - к возникновению колебаний.
Время разогрева —время междуподачей на датчик электрического напряжения или сигнала возбуждения и моментом, когда датчикначинает работать, обеспечиваятребуемую точность измерений. Многие датчики обладают несущественным временем разогрева. Однако некоторыедетекторы, особенно работающие в устройствах с контролируемой температурой(термостатах), для своего разогрева требуют секунды, а то и минуты.
В теории автоматическогоуправления (ТАУ) принято описывать взаимосвязь междувходами и выходами устройства в виде линейных дифференциальных уравнений с постоянными коэффициентами. Очевидно, чтопри решении таких уравнений можно определить динамические характеристикиустройства. В зависимости от конструкцийдатчиков, уравнения, описывающие их, могут иметь разный порядок.
Датчики нулевого порядка - имеют линейную передаточную функцию и могут быть описаны следующейзависимостью от времени:
S(t)=a + bs(t).
Коэффициент а называется смещением, b— статической чувствительностью. Из вида уравнения видно, что оноописывает датчики в состав которых не входят энергонакопительные элементы, такие какконденсаторы или массы. Датчики нулевого порядка относятся к устройствам мгновенного действия.Иными словами, у таких датчиков нет необходимости определять динамическиехарактеристики.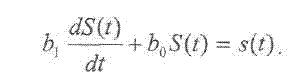
Датчики первого порядка - содержат один энергонакопительный элемент ихарактеризуется уравнением вида:
Типичный пример датчика первогопорядка - датчик температуры, в котором роль энергонакопительного элемента играет теплоемкость.Дляописания датчиков первого порядка существуетнесколько способов.
Частотная характеристика - наиболее часто используемый способ описания инерционностидатчиков - показывающая насколько быстродатчик может среагировать на изменение внешнего воздействия.
Дляотображения относительногоуменьшения выходного сигнала при увеличении частоты применяетсяамплитудно-частотная характеристика. Для описания динамических характеристик датчиков частоиспользуется граничная частота,соответствующая 3-дБ снижению выходного сигнала, показывающая на какой частоте происходит 30%уменьшение выходного напряжения или тока.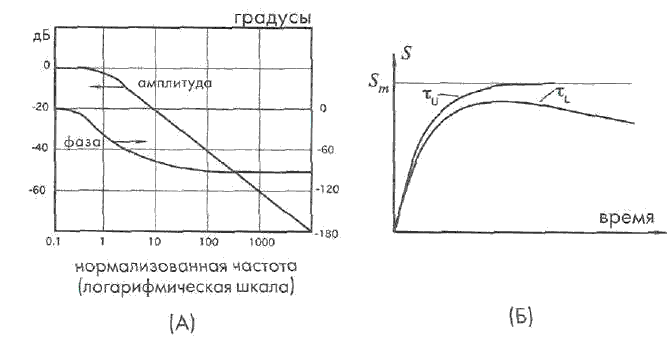
Частотные характеристики:
А - частотнаяхарактеристика датчика первогопорядка,
Б - частотная характеристика датчика с ограничениями по верхней и нижней частоте среза, где ?u и ?r -соответствующие постоянные времени
Эта граничная частота называется верхней частотой среза,считается предельнойчастотой работы датчика.
Быстродействие датчика – скорость его реакции, выражаемаяв единицах внешнего воздействия на единицу времени. Способ описания: АЧХ или быстродействие, зависит от типа датчика, областиприменения и предпочтений разработчика.
Другой способ описания быстродействиязаключается в определении времени, требуемого для достижения выходным сигналомдатчика уровня 90% от стационарногоили максимального значения при подаче на его вход ступенчатого внешнеговоздействия.
Постоянная времени - мера инерционностидатчика. Широко используется для датчиков первого порядка.Втерминах электрических величин она равна произведению емкости на сопротивление: ? = CR. В тепловых терминах под С и R понимаются теплоемкость и тепловоесопротивление. Как правило, постоянная времени довольно легко измеряется. Временная зависимостьсистемы первого порядкаимеет вид:![]()
S/Sm=1-1/е = 0,6321
Т.е. поистечении времени, равного постоянной времени, выходной сигнал датчика достигает уровня,составляющего приблизительно 63% от установившегося значения. Аналогично можно показать, что поистечении времени, равного двум постоянным времени, уровень выходного сигналасоставит 86.5%, а после трех постоянных времени - 95%.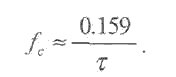
Частота среза – наименьшая или наибольшая частота внешних воздействий, которую датчик можетвоспринять без искажений. Верхняя частота среза показывает насколько быстро датчик реагирует навнешнее воздействие, а нижняя частота среза -с каким самым медленным сигналом он может работать. На практике для установления связи между постоянной времени датчика первого порядка и его частотой среза fc, как верхней так и нижней, используют простую формулу:
Фазовый сдвиг - на определенной частоте показывает насколько выходнойсигнал отстает от внешнего воздействия. Сдвиг измеряется либо в градусах, либов радианах и обычно указывается для датчиков, работающих с периодическимисигналами. Если датчик входит в состав измерительной системы с обратными связями, всегда необходимо знать его фазовыехарактеристики. Фазовый сдвиг датчика можетснизить запас по фазе всей системы в целом и привести к возникновению нестабильности.
Датчики второгопорядка описывают поведение датчиков с двумя энергонакопительными элементами(и описываются дифференциальными уравнениями второго порядка):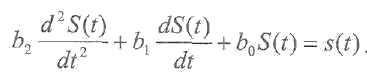
Примером датчика второго порядка является акселерометр, всостав которого входитмасса и пружина.Навыходах датчиков второго порядка после подачи на их входы ступенчатого воздействия практически всегдапоявляются колебания. Эти колебания могут быть очень кратковременными, тогда говорят, что датчикдемпфирован, или могут длиться продолжительное время, а то и постоянно. Продолжительные колебанияна выходе датчикаявляются свидетельством его неправильной работы.
Резонансная(собственная) частота – частота датчика второго порядкавыражается в герцах или радианах в секунду. На собственной частоте происходит значительное увеличение выходного сигналадатчика. Обычно производители указываютзначение собственной частоты датчика и его коэффициент затухания (демпфирования). От резонансной частотызависят механические, тепловые и электрические свойства детекторов. Обычнорабочий частотный диапазон датчиков выбирается либо значительно нижесобственной частоты (по крайней мере на 60%), либо выше ее. Однако для некоторых типов датчиков резонансная частотаявляется рабочей. Например, детекторыразрушения стекла, используемые в охранных системах, настраиваются на узкую полосу частот в зоне частоты резонанса,характерную для акустическогоспектра, производимого разбивающимся стеклом.
Демпфирование - это значительное снижение или подавление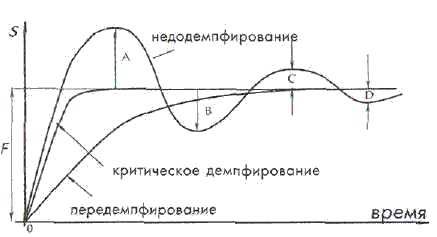 колебаний в датчиках второго и более высоких порядков. Когдавыходной сигнал устанавливается достаточнобыстро и не выходит за пределы стационарного значения, говорят, что система обладает критическим затуханием, а ее коэффициентдемпфирования равен 1. Когдакоэффициент затухания меньше 1, и выходной сигнал превышает установившееся значение, говорят, что системанедодемфирована. А когда коэффициент затухания больше 1, и сигналустанавливается гораздо медленнее, чем в системес критическим затуханием, говорят, что система передемпфирована.
колебаний в датчиках второго и более высоких порядков. Когдавыходной сигнал устанавливается достаточнобыстро и не выходит за пределы стационарного значения, говорят, что система обладает критическим затуханием, а ее коэффициентдемпфирования равен 1. Когдакоэффициент затухания меньше 1, и выходной сигнал превышает установившееся значение, говорят, что системанедодемфирована. А когда коэффициент затухания больше 1, и сигналустанавливается гораздо медленнее, чем в системес критическим затуханием, говорят, что система передемпфирована.
Дляколебательного выходного сигнала коэффициент затухания или демпфирования определяетсяабсолютным значением отношения большей амплитуды к меньшей пары последовательновзятых полуволн колебанийотносительно установившегося значения, т.е. можно записать: коэффициент демпфирования =F/A = A/B = B/C=….
Возможные варианты выходных сигналовдатчиков в ответ на ступенчатое внешнее воздействие.Варианты выходныхсигналов:
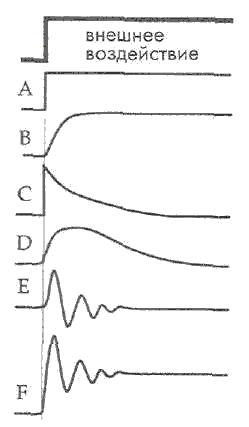 А - бесконечные верхняя и нижние частоты,
А - бесконечные верхняя и нижние частоты, В- система первого порядка с ограниченной верхнейчастотой среза,
С - система первого порядка с ограниченной нижней частотой среза,
D - система первого порядка с ограниченными верхней и нижней частотамисреза,
Е - система с узкой полосой частот (резонанснаясистема),
F - широкополосная система с резонансом.